Парадокс нарушения вероятности (развитие игры Пенни)
Аннотация: Новые экспериментальные законы теории вероятности изменят те практики и теории, где теория вероятности основной математический аппарат. Описано новое открытие, которое вошло в список парадоксов теории вероятности. Это открытие – алгоритм, игра «Фила 2», который управляет получением нужного вероятностного результата. Алгоритм позволяет вместо одной, строго определённой вероятности, получать диапазон вероятностей, из которых можно подбирать более удобную для получения нужного практического результата.
Введение

Обнаружение каждого нового парадокса – это новая возможность развить и уточнить научные теории. За последний век в теории вероятности появилось несколько парадоксов, на взгляд автора наиболее интересные из них: парадоксальная «Игра Пенни» [1, 2] и парадокс Монти Холла. Теперь к ним добавляется новый парадокс, который по сложившийся традиции, представлен в виде парадоксальной игры «Фила 2». Парадокс «Фила 2» — это алгоритм нарушения равновероятного угадывания бинарного 2 элементарного события (сторон выпашей монеты). То есть, при применении этого алгоритма исчезает равная вероятность угадывания каждой стороны монеты. Пока затруднительно этому дать объяснение. Этот эффект проявляется только при выполнении требований алгоритма «Фила 2», при любых других ранее предлагаемых алгоритмах угадывания выпавшей стороны монеты вероятность угадывания обоих сторон оставалась в рамках классической теории вероятности, то есть каждая из сторон монеты обладала вероятностью угадывания равной 0,5.
Можно делать разные предположения, что в философском смысле значит результат алгоритма «Фила 2». Например, что действительно существуют какие-то последовательности действий, о которых говорила алхимия (которые сейчас воспринимаются в виде технологий), и эти последовательности действий можно подобрать для получение желаемого. Или, что сторонники того, что предшествующие события влияют на вероятность обнаружения последующих выпадающих событий, наконец получили этому подтверждение. На первоначальном этапе осмысления алгоритма управления вероятности выпавшей стороны монеты можно делать совершенно разные предположения.
Нужно отметить, что первым алгоритмом управления вероятностью угадывания событий в случайном бинарном потоке был алгоритм парадоксальной игры Пенни. Он приводит в недоумение тем, что демонстрирует полное отрицание случайности при подбрасывании монеты в серии игр (имеется в виду, что если требования алгоритма Пенни соблюдаются, то многократно повторяемая игра приводит по сумме побед к стопроцентному выигрышу игрока применившего «тайные знания» алгоритма Пенни). То есть алгоритм игры Пенни превращает не предсказуемый, равновероятный, результат подбрасывания монеты на полностью предсказуемый, победный результат, по итогу серии игр (Алиса и Боб играют 21 партию, как в настольном теннисе, побеждает всегда применяющий алгоритм Пенни, он первый всегда набирает 21 победу).
К недостаткам алгоритма Пенни относится то, что нельзя делать прямое предсказание на то, какой стороной выпала монета. Это недостаток устраняет алгоритм в парадоксальной игре «Фила 2», в которой именно управляется величина вероятности угадывания стороны выпашей монеты (состояния равновероятных дискретных случайных бинарных элементарных событий стохастического потока).
Основная часть
Рассмотрим таблицу 1 с результаты применения алгоритма игры «Фила 2» по изменению вероятности угадывания реализовавшихся дискретных равновероятных бинарных состояний стохастического потока (последовательных выпадений сторон монеты), где под «0» и «1» понимаются стороны честной монеты. В ней показано, что при угадывании состояний «0» и «1», по правилам игры, вероятностью угадывания можно управлять в диапазоне от 0,25 до 0,75. Ознакомимся правилами игры.
Правила игры «Фила 2»
Играют двое (как в «Парадоксе Монти Холла») Алиса и Боб. Алиса подбрасывает монету и записывает в строчку выпадения её сторон (которые мы обозначим как «0» и «1»). Самое последнее выпавшее состояние: e(t2) Алиса дописывает слева от предыдущего состояния: e(t1).
| Серии e(t2); e(t1) | Число серий | Вероятность угадывания: «1»; «0» в «Фил 2» | Вероятность угадывания по действующей ТВ |
| 11 | Угадано «1»: 1669449 | 0,25 | 0,50 |
| 10 | Угадано «0»: 4998621 | 0,75 | 0,50 |
| Событий в бинарной последовательности 1 и 2 по 20 000 000. Сумма спектров «11 + 10»: 6668070. | |||
Вся игра сосредоточена в области двух последних впадений монеты, только они учитываются в игре. Алиса подбрасывает монету до тех пор, пока она не выявит одно из двух искомых состояний: «11» или «10» (пока она не встретит первую «1», перед которой уже что-то выпало: либо «0», либо «1»). После этого она просит угадать Боба, что выпало перед последней единицей: «0» или «1». После ответа Боба Алиса увеличивает счёт угаданных предсказаний, либо счёт не угаданных предсказаний.
Парадоксальность игры «Фила 2» заключается в том, что перед последней «1», нули и единицы не образуются с равной вероятностью, их вероятность угадывания будет разной, что и показано в таблице 1. Нули образуются с вероятностью в три раза большей, чем единицы.
Таблица 1 была получена на основе компьютерного эксперимента, смотри рисунок 1. В этом эксперименте было сымитировано устройство, генерирующее дискретные, равновероятные случайные бинарные события. Эти события в порядке их образования поступали на анализатор их состояний – Алиса. При выпадении условной «1» Алиса приостанавливала просмотр ленты событий и Боб делал предсказание. Для получения значений таблицы 1 компьютерный эксперимент был проведён дважды. В первом эксперименте был организован поток из 20000000 бинарных событий, Боб всегда предсказывал единицу «1», и угадал 1669449 раза. Во втором эксперименте был то же организован поток из 20000000 бинарных событий, Боб всегда предсказывал нуль «0», и угадал 4998621 раза (в 3 раза больше).
Был также поставлен третий компьютерный эксперимент, в котором на потоке из 20000000 бинарных событий Алиса производила одновременный поиск двух шаблонов (серий) «11» и «10». В этом совместном поиске Алиса зафиксировала: серию «11» -1668828 раз, серию «01» - 4997884 раза, их общая сумма - 6666712. То есть, значения таблицы 1 были подтверждены в третьем эксперименте, в котором производился одновременный поиск серий «11» и «10». Подтверждение численностей находимых серий в трёх бинарных потоках говорит о том, что механизм парадокса игра «Фила 2» является иным, чем механизм парадокса в игре Пенни. В игре Пенни победа одного шаблона над другим сопровождается изменением численностей конкурирующих друг с другом серий, при одновременном поиске двух серий. В игре «Фила 2» изменение количества серий при их одновременном поиске не происходит, численность серий остаётся такой же, как и при раздельном поиске каждой серии (смотри таблицу 1).
Игра «Фила 2» симметрична относительно «0» и «1». То есть, при замене последней «1» на «0» вероятность появления перед нулём единиц будет также в три раза больше, чем вероятность появления перед нулём нуля.
Игра «фила 2» описывает физический процесс, который представлен на рисунке 1 при помощи персонажей Алисы (устройство, объект «А») и Боба (устройство, объект «Б»), которые стали стандартом для пояснения сложных понятий из квантовой механики, в частности они широко применяются в рисунках по пояснению квантовой запутанности.
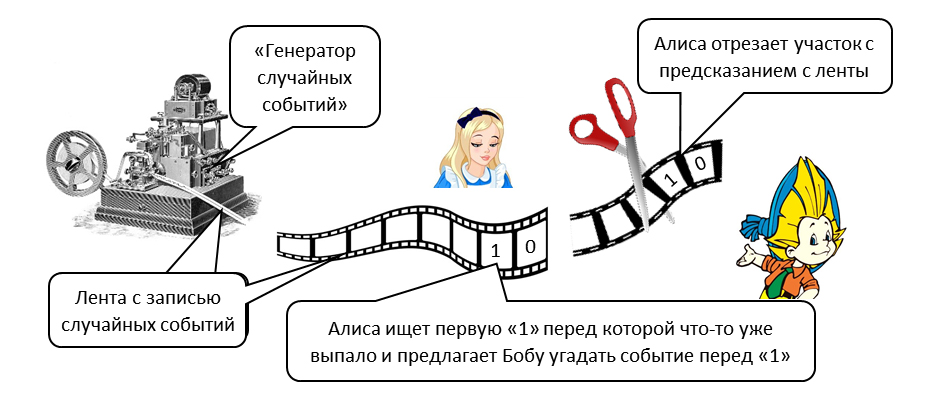
Рисунок 1. «Организация средств и действий в алгоритме игра «Фила 2». Игра «Фила 2» может быть реализована как на компьютере, так и проводится в настольном варианте (для этого нужны всего две монеты).
Компьютерный вариант игры «Фила 2»
Возможный вид компьютерной игры приведён на рисунке 2. Статистика по созданным случайным «0» и «1» и победам отображается на экране. Создаваемые генератором случайных событий нули «0» и единицы «1» отображаются в порядке их создания в одной строке.
Настольный вариант игры «Фила 2»
В игру «Фила 2» так же легко играть, как и в классическую орлянку. Для физической игры «Фила 2» нужно всего две монеты. Надо по очереди подбрасывать эти монеты, пока на последней подброшенной монете не выпадет условная «1», после чего угадывающего игрока просят угадать, что выпало на предыдущей монете. Подбрасывать монеты до угадывания долго не нужно, так как серии до выпадения условной «1» получаются короткие (смотри рисунок 2).
Обсуждение
Парадоксальная игра «Фила 2» содержит в себе черты двух широко известных парадоксов: парадокса Монти Холла и парадоксальной игры Пенни.
Сравнение парадокса «Фила 2» и парадокса Монти Холла
В парадоксе «Фила 2» задействованы то же два человека как в парадоксе Монти Холла. В парадоксе Монти Холла ведущей не только обладает всей полнотой информации, но и непосредственно сам, уменьшает неопределённость, организует условие для изменения вероятности угадывания для угадывающего игрока. В отличие от парадокса Монте Холла, от ведущего в парадоксе «Фила 2» вероятность совершенно не зависит, он её не меняет. В парадоксе «Фила 2» ведущий рутинно выявляет комбинацию, в которой перед только что выпавшей единицей должно находится ещё одно, причём любое, выпадение (либо «0», либо «1») и предлагает угадывающему игроку угадать, что за событие выпало перед единицей. Как видно, общее в функциональности ведущего в парадоксах Монте Холла и «Фила 2» то, что оба ведущих обладают всей полнотой информации. Общее в функциональности угадывающих игроков: в парадоксах Монте Холла и «Фила 2» то, что они находятся в состоянии полного неведения.
Сравнение парадоксальных игр «Фила 2» и игры Пенни
Как в парадоксальной игре Пенни, так и в парадоксальной игре «Фила 2» делаются ставки на выпадение комбинаций. В обоих играх в качестве источника случайных событий служит поток дискретных бинарных событий (например выпадение сторон монеты). На этом сходство заканчивается, так как в парадоксальной игре Пенни нет возможности угадывать выпадение стороны одной отдельной монеты, а для парадоксальной игры «Фила 2» это основной способ демонстрации парадокса нарушения равной вероятности угадывания сторон монеты.
Игра «Фила 2» является следствием развития «Комбинаторики длинных последовательностей» [3,4,5] и предыдущих парадоксальных игр созданных на основе «Комбинаторики длинных последовательностей» [6,7,8].
Управление вероятностью угадывания выпавшей стороны монеты
При решении споров случайное выпадение стороны монеты, в прошлые века, воспринималось как указание от Бога, на чей Он стороне. Такое восприятие выпадение стороны монеты (воля богов) было вызвано тем, что не смотря на все попытки людей найти способы угадать сторону выпавшей монеты, эти способы так и не были найдены, до появления алгоритма игры «Фила 2».
В таблице 1 вероятность угадывания монеты находится в диапазоне: 0,25 – 0,75. Значит вероятность угадывания выпавшего значения можно менять в игре «Фила 2» внутри всего диапазона вероятностей: 0,25 – 0,75.
Для угадывания с вероятностью 0,75 нужно всё время предсказывать условный «0».
Для угадывания с вероятностью 0,25 нужно всё время предсказывать условную «1».
Для получения вероятности угадывания лежащей внутри диапазона 0,25 – 0,75, нужно чередовать предсказания «0» и «1» в разных пропорциях.
Для получения вероятности угадывания больше 0,5 необходимо чаще предсказывать выпадения «0» чем «1».
Для получения вероятности угадывания меньше 0,5 необходимо чаще предсказывать выпадения «1», чем «0».
Для получения вероятности угадывания 0,5 необходимо одинаково часто предсказывать выпадения «1» и «0».
Выводы
- «Игра Фила 2» — это первый в мире алгоритм, который меняет величину вероятности угадывания дискретных событий равновероятного бинарного потока (выпавшей стороны монеты).
- Описан алгоритм «Игры Фила 2».
- Описан способ управления угадывания выпавшей стороны монеты в диапазоне вероятностей от 0,25 до 0,75.
Литература
- Walter Penney, 95 Penney-Ante, Journal of Recreational Mathematics, 2 (1969), 241.
- Гарднер Мартин. Путешествие во времени = Time Travel and Other Mathematical Bewilderments. — М.: «Мир», 1990. — С. 75. — 341 с. — ISBN 5-03-001166-8.
- Филатов О. В., Филатов И.О., Макеева Л.Л. и др. «Потоковая теория: из сайта в книгу». Москва, «Век информации», 2014, с.200, ISBN 978-5-906511-06-5.
- Филатов О. В., Филатов И.О., статья «О закономерностях структуры бинарной последовательности», «Журнал научных публикаций аспирантов и докторантов», №5 (95), 2014 г., с.226-233.
- Филатов О. В., Филатов И.О. «Закономерность в выпадении монет – закон потоковой последовательности». Германия, Издательский Дом: LAPLAMBERT Academic Publishing, 2015, с. 268, ISBN 978-3-659-71144-2.
- Филатов О. В., статья «Техника управления вероятностью обнаружения элементарных событий - «0», «1» (аналоги сторон монеты) через псевдозапутывание случайных последовательностей по правилам парадоксальной игры Пенни», «Проблемы современной науки и образования», № 10 (92), 2017 г., с.10-18.
- Филатов О.В., Филатов Л.О., статья «Нетранзитивные технологии изменения вероятности в игре пенни и в игре фила», «Вестник науки», № 7 (64), т. 4. 2023 г. с. 311-329.
- Филатов О.В., статья «Количественный расчёт результатов парадоксальной игры Пенни (управляемая вероятность выпадений серий монеты) на ставках минимальной длины», «Проблемы современной науки и образования», № 17 (99). 2017 г., с. 6-19.
